728x90
서론
백준 1717번 문제를 몇 시간동안 못풀어서 결국 구글링을 해봤는데, 이 문제는 Union-find알고리즘을 써야한다는 걸 알게되었다. Union-Find 알고리즘을 처음 접했을 땐 너무 참신해서 짜릿했다! 이 알고리즘을 정리해두면 나중에도 유용하게 쓰일 것 같아 글을 포스팅한다
Disjoint Set(서로소 집합)이란?

- Union-find 알고리즘은 Disjoint set을 표현할 때 사용된다
- Disjoint는 "뿔뿔이 흩어지다"라는 뜻이다
- Disjoint set은 공통원소가 없는 집합을 뜻한다
- (백준 1717번 문제는 Disjoint Set이 주어진다)
Union-Find 알고리즘이란?
- Disjoint Set(서로소 집합)을 효율적으로 표현하는 알고리즘이다
- 집합을 트리구조로 표현한다
- 각 값이 자신의 부모를 저장하고 있다
- 최고 조상이 같다면 같은 집합임을 알 수 있음
- 아래 그림과 같은 느낌으로 생각하면 된다
- 최고 조상의 부모는 자기자신
- 각 노드(인덱스)는 자신의 부모를 저장
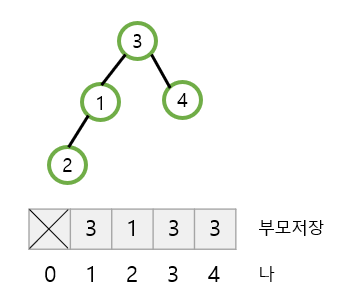
Union-Find 알고리즘 연산종류
- Union-Find 연산은 ①합하기(union)와 ②찾기(find) 연산으로 이루어진다
1. 합하기(Union) 연산

- 합하기 연산을 수행하면 이렇게 트리처럼 줄줄 매달라게 된다
- 각 노드는 자신의 부모정보를 가지고 있고, 최상위 부모는 자기 자신을 부모로 가진다
- x와 y를 union한다면
- x의 최상위 부모 x'를 찾고
- y의 최상위 부모 y'를 찾아서
- x'의 부모를 y'로 설정해주면 됨
- Union(2, 3)의 결과는 2의 최상위 부모인 1과 3의 최상위 부모인 3을 연결해주는 걸 볼 수 있음
2. 찾기(find) 연산
- 자신의 최상위 부모를 찾는 연산이다
- 재귀방식으로 어렵지 않게 구할 수 있음
- (부모의 부모의 부모의... )
- 만약 자신의 부모가 자기자신이 아니라면 자기 부모로 find를 재귀호출
- 자기자신이라면 return
- 최상위 조상이 같으면 같은 집합에 속하는 거다
구현 코드
int find(int x) {
if (x == parent[x])
return x;
else
return find(parent[x]);
}
void union(int x, int y) {
x = find(x);
y = find(y);
parent[y] = x;
}- find: 부모를 따라올라가면서 최상위 조상 찾기
- union: 두 개의 최상위 조상을 찾고, 최상위 조상 중 하나의 부모를 다른 최상위 조상으로 만들어주기
Union-Find 최적화가 필요한 이유
위 연산대로만 구현한다면 문제의 답을 구할 수는 있다. 하지만 최악의 상황을 가정해보자

- 숫자가 많아질수록 트리깊이는 끝없이 길어질 수 있다
- 트리의 깊이가 깊어지면 성능은 점점 떨어진다
- union연산을 할 때도 트리의 높이 h만큼 올라가야하고
- find연산을 할 때도 트리의 높이 h만큼 올라감
- 트리의 높이가 몇 백이 된다면? => 답이 없다!!
- (잘 와닿지 않는다면 백준 1717번 문제를 최적화없이 풀어보면 된다! 몸으로 느낄 수 있음)

Union-Find 최적화 방법
1. Find연산의 최적화
- find를 할 때 트리의 높이를 압축하는 아이디어이다

- 7이 이렇게 밑에 달려있을 때, 7의 최고 조상인 3을 찾으면 오른쪽처럼 트리가 압축된다!
- 이게 어떻게 가능한지는 코드를 보면서 이해해보자
int find(int x) {
if (x == parent[x])
return x;
parent[x] = find(parent[x]);
return parent[x];
}- 이전코드에서 parent[x]를 최고조상으로 바꿔주는 중간코드를 추가했다
- 이렇게 되면 재귀적으로 최고조상을 찾음과 동시에 내 모든 조상의 부모가 최고조상으로 갱신된다

- 찾기: 7 -> 6찾음 -> 5찾음 -> 3찾음(최고조상)
- 갱신: 3찾음 -> 5의 부모 갱신 -> 6 부모 갱신 -> 7 부모 갱신
2. Union 연산의 최적화
- 트리 높이를 저장할 배열 rank[]를 만듦
- 최고조상에게 해당 트리의 높이를 저장함
- 최상위 조상 둘을 찾아서 부모를 갱신할 때, 자식이 적은 쪽의 부모를 많은 쪽으로 갱신하는 아이디어
int[] rank = new int[N + 1];
...
a = find(a);
b = find(b);
if (a != b) {
if (rank[a] < rank[b]){ //자식이 많은 쪽이 최고조상, 적은 쪽의 부모를 갱신
parent[a] = b;
if (rank[a] == rank[b]) //같으면 최고조상의 랭크를 1 증가
rank[b]++;
} else {
parent[b] = a;
}
}- 다음과 같이 최고조상의 랭크를 비교하여 높이가 낮은쪽을 갱신한다
- 이렇게 되면 트리의 높이를 조금은 낮게 유지 가능
활용: 백준 1717 집합의 표현 - 골드5
https://www.acmicpc.net/problem/1717
1717번: 집합의 표현
초기에 $n+1$개의 집합 $\{0\}, \{1\}, \{2\}, \dots , \{n\}$이 있다. 여기에 합집합 연산과, 두 원소가 같은 집합에 포함되어 있는지를 확인하는 연산을 수행하려고 한다. 집합을 표현하는 프로그램을 작
www.acmicpc.net
- 4시간 넘게 못풀었던 문제...ㅠㅠ
- set을 사용하면 메모리 초과
- 최적화 union-find 를 사용하지 않으면 시간 초과
- 이제 나는 Union-Find를 아니까 아주아주 쉽게 풀 수 있다! ㅎㅎㅎ
풀이 코드
import java.io.BufferedReader;
import java.io.IOException;
import java.io.InputStreamReader;
import java.util.StringTokenizer;
public class Main {
static int[] parent;
public static void main(String[] args) throws NumberFormatException, IOException {
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
StringTokenizer st = new StringTokenizer(br.readLine());
int N = Integer.parseInt(st.nextToken());
int M = Integer.parseInt(st.nextToken());
parent = new int[N + 1];
for (int i = 1; i <= N; i++)
parent[i] = i;
StringBuilder sb = new StringBuilder();
for (int i = 0; i < M; i++) {
st = new StringTokenizer(br.readLine());
int command = Integer.parseInt(st.nextToken());
int a = Integer.parseInt(st.nextToken());
int b = Integer.parseInt(st.nextToken());
if (command == 0) {
a = find(a);
b = find(b);
if (a != b) //부모가 같을 땐 갱신 ㄴㄴ
parent[b] = a;
}
else if (command == 1) {
a = find(a);
b = find(b);
if (a == b)
sb.append("YES").append("\n");
else
sb.append("NO").append("\n");
}
}
System.out.print(sb);
}
// x의 부모를 찾는 연산
public static int find(int x) {
if (x == parent[x])
return x;
//제일 조상을 부모로 바꿔끼우기
parent[x] = find(parent[x]);
return parent[x];
}
}- find 최적화만 사용해준 코드다
- parent배열을 0부터 N인덱스까지 초기화해줌
- 초기화: 부모를 자기자신으로 설정
- command별로 구분해서 동작을 수행
- 합치기(0): 각 최고조상을 찾아서 한쪽 부모를 갱신 (최고조상이 같으면 갱신 필요 x)
- 같은 집합인지 확인(1): 각 최고조상을 찾고, 둘이 같은지 비교


find최적화 rank배열이 오히려 시간이 더 걸렸다! rank를 만들고/ 비교하고/ 갱신하는 오버헤드가 더 컸던 것 같기도 함
참고자료
https://gmlwjd9405.github.io/2018/08/31/algorithm-union-find.html
728x90
'프로그래밍 언어 > Java' 카테고리의 다른 글
| [Java] 자바 코드 컨벤션 정리(Google Java Style Guide) (0) | 2023.10.18 |
|---|---|
| [JAVA] StringBuffer와 StringBuilder의 차이점 (0) | 2023.10.11 |
| [JAVA] 최소힙, 최대힙 사용법 정리(PriorityQueue) (0) | 2023.10.06 |
| [JAVA] 이진탐색 lowerbound, upperbound 정리 (0) | 2023.10.01 |
| Arrays.binarySearch 메서드 알아보기 (2) | 2023.09.30 |
